行列積の計算順序を減らす方法!高速化テクニック
行列積の計算は、計算量が膨大になりやすい問題の一つです。特に大規模な行列を扱う際には、計算にかかる時間やリソースが大きく影響する可能性があります。この記事では、行列積の計算順序を最適化する方法について解説します。行列の順序を効果的に変更することで、計算時間を大幅に短縮し、性能を向上させることができます。ここでは、具体的なテクニックやアルゴリズム、実践的なアプローチを紹介します。
行列積の計算順序を減らす方法!高速化テクニック
行列積の計算は、多くの科学計算やデータ分析の分野で重要な役割を果たします。しかし、大きな行列の場合は計算時間が長くなることがあります。ここでは、行列積の計算順序を最適化して、高速化テクニックを紹介します。
行列積の基本的な計算方法を理解する
行列積の計算は、2つの行列を乗じて新しい行列を生成する操作です。行列 A と行列 B の積 C は次のように計算されます。
| 計算 | 説明 |
|---|---|
| $$ C {ij} = sum {k=1}^{n} A {ik} B {kj} $$ | 行列 C の (i, j) 要素は、行列 A の i 行と行列 B の j 列の内積の和です。 |
この基本的な計算方法を理解することで、どのように計算順序が計算時間を影響するかが明確になります。
BIOS起動しないPCを修理!自分でできる対処法行列のサイズに基づく最適化
行列のサイズによって、計算順序が大きく変化します。たとえば、3つの行列 A, B, C の積を計算する場合、以下のように2つの方法があります。
| 計算順序 | 計算量 |
|---|---|
| (A × B) × C | $$ (n times m) times (m times p) times (p times q) = nmp + npq $$ |
| A × (B × C) | $$ (n times m) times (m times p) times (m times q) = mnp + mpq $$ |
ここで、計算量が最小になる計算順序を選択することが重要です。
行列の対称性や特殊性を利用する
行列が対称行列や対角行列などの特殊な形をしている場合、計算を大幅に省略することができます。例えば、対角行列と一般行列の積は、対角行列の対角要素に一般行列の各列を乗じるだけの簡単な操作で済みます。
| 行列の種類 | 利用可能なテクニック |
|---|---|
| 対角行列 | 対角要素との乗法のみ |
| 対称行列 | 半分の計算で済む |
| 三角行列 | 部分的な計算で済む |
これらの特殊性を利用することで、計算時間を大幅に削減できます。
Joyo銀行アプリ英語エラー解決!トラブルシューティング並列計算の活用
行列積の計算は、並列化が可能な操作です。現代のコンピュータは、複数のコアを持つことが多く、複数の計算を同時に実行することができます。並列計算を利用することで、計算時間を大幅に短縮できます。
| 並列計算方法 | メリット |
|---|---|
| マルチスレッド | 複数のコアを活用 |
| GPU利用 | 多くの並列計算ユニットを活用 |
| 分散処理 | 複数のコンピュータを活用 |
並列計算の活用は、特に大きな行列や複雑な計算で大きな効果が期待できます。
アルゴリズムの選択と最適化
行列積の計算には、さまざまなアルゴリズムが存在します。例えば、Naiveなアルゴリズム、Strassenアルゴリズム、Coppersmith-Winogradアルゴリズムなどがあります。これらのアルゴリズムには、それぞれ特徴的な計算量と実装の難しさがあります。
| アルゴリズム | 計算量 | 実装の難しさ |
|---|---|---|
| Naiveアルゴリズム | $$ O(n^3) $$ | 簡単 |
| Strassenアルゴリズム | $$ O(n^{2.81}) $$ | 中程度 |
| Coppersmith-Winogradアルゴリズム | $$ O(n^{2.376}) $$ | 難しい |
アルゴリズムの選択と最適化は、計算時間を大幅に短縮する上で重要な要素です。
Amazon CS11エラー解決!原因と対策を徹底解説キャッシュブロッキングとは何ですか?
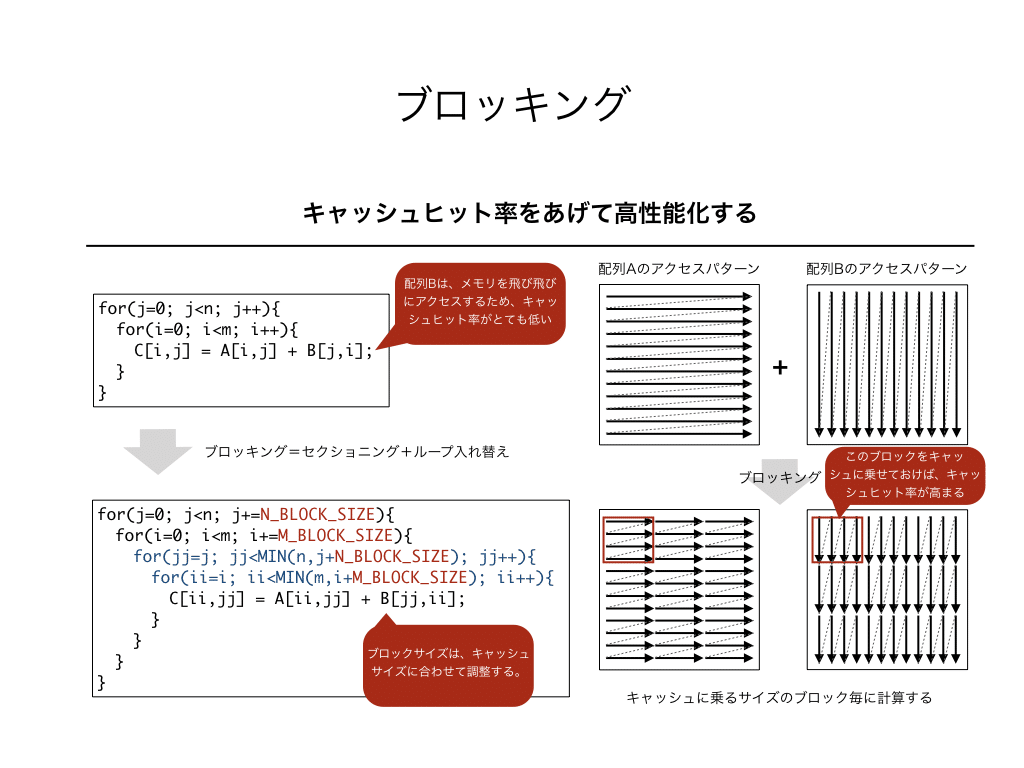
キャッシュブロッキングとは、ウェブサイトのパフォーマンスを最適化するために使用されるテクニックの一つです。キャッシュとは、ウェブブラウザがウェブページのリソースを一時的に保存する場所を指します。これらのリソースには、画像、CSS、JavaScriptなどが含まれます。キャッシュブロッキングは、これらのリソースがブラウザのキャッシュに保存されないようにするために使用されます。これにより、ユーザーがウェブページを再度訪れた際に、最新のコンテンツが常に表示されるようにすることができます。
キャッシュブロッキングの目的
キャッシュブロッキングの主な目的は、ウェブサイトのコンテンツが常に最新の状態であることを保証することです。これには以下のような利点があります:
- 最新のコンテンツの表示:ユーザーがウェブページを訪れるたびに、最新のコンテンツが表示されるため、情報を常に新鮮に保つことができます。
- 信頼性の向上:ユーザーが古くなったコンテンツを表示することを防ぐことで、ウェブサイトの信頼性を高めることができます。
- 開発者にとっての恩恵:コンテンツの更新が即座に反映されるため、開発者がより効率的に作業を行えるようになります。
キャッシュブロッキングの実装方法
キャッシュブロッキングを実装するには、主に以下のような方法があります:
Resonaアプリ問題解決!トラブルシューティングガイド- URLの変更:ファイルのURLにバージョン番号やタイムスタンプを追加することで、ブラウザが新しいリソースを読み込むように誘導します。
- HTTPヘッダーの設定:サーバーから送信されるHTTPヘッダーを調整し、キャッシュの有効期間を短く設定することで、ブラウザが頻繁にサーバーに確認を行うようにします。
- ETagの使用:ETag(Entity Tag)は、リソースの一意性を確認するための識別子です。ETagを使用することで、ブラウザがサーバーにリソースが更新されたかどうかを確認できます。
キャッシュブロッキングの影響
キャッシュブロッキングには、ウェブサイトのパフォーマンスやユーザーエクスペリエンスに影響を与えるいくつかの効果があります:
- 初期ロード時間の改善:ユーザーが初めてウェブページを訪れる際に、キャッシュが利用できないため、初期ロード時間が若干長くなる可能性があります。
- サーバー負荷の増加:ブラウザが頻繁にサーバーにリクエストを送信することで、サーバーの負荷が増加する可能性があります。
- ユーザーの満足度向上:常に最新のコンテンツが表示されることで、ユーザーの満足度が向上し、ウェブサイトの評判が向上する可能性があります。
行列計算の積の順番は?

行列計算の積の順番は、左から右に計算します。つまり、行列積 ( AB ) において、まず行列 ( A ) と行列 ( B ) の対応する要素を乗算し、その結果を合計することで各要素が得られます。行列の積は 結合的 ですが、交換的 ではありません。つまり、 ( AB ) は一般的に ( BA ) と等しくないことがありますが、 ( (AB)C ) は ( A(BC) ) と等しいです。
行列の積の定義
行列の積は、2つの行列 ( A ) と ( B ) が 互いに乗算可能 であるとき定義されます。つまり、行列 ( A ) の列数が行列 ( B ) の行数と等しい場合、積 ( AB ) が計算できます。結果の行列 ( AB ) の行数は行列 ( A ) の行数に等しく、列数は行列 ( B ) の列数に等しいです。
- 行列 ( A ) が ( m times n ) 行列で、行列 ( B ) が ( n times p ) 行列である場合、積 ( AB ) は ( m times p ) 行列になります。
- 行列 ( A ) の各行の要素と行列 ( B ) の各列の要素の 内積 を計算します。
- 計算結果は新しい行列の各要素として配置されます。
行列の積の性質
行列の積にはいくつかの重要な性質があります。特に、結合的性質と交換的性質に注目することが重要です。
- 結合的性質: 3つの行列 ( A ), ( B ), ( C ) について、 ( (AB)C = A(BC) ) が成り立ちます。
- 交換的性質: 一般的に、2つの行列 ( A ) と ( B ) の積は交換的ではありません。つまり、 ( AB neq BA ) であることが多いです。
- 単位行列との積: 任意の行列 ( A ) について、単位行列 ( I ) との積は、 ( AI = IA = A ) が成り立ちます。
行列の積の応用
行列の積は、様々な分野で重要な役割を果たします。線形代数、コンピューターサイエンス、物理学など、多くの応用例があります。
- 線形変換: 行列の積は、ベクトルの線形変換を表すために使用されます。例えば、回転や拡大縮小などの変換を行列の積で表現できます。
- システムのモデル化: 複雑なシステムをモデル化する際に、行列の積が使用されます。例えば、電気回路の解析や経済モデルなどにおいて、行列の積は重要なツールとなります。
- データ処理: 機械学習やデータ分析において、行列の積は特徴量の抽出やデータの変換に用いられます。特に、行列の 固有値分解 や 特異値分解 は、データの圧縮や特徴の抽出に有効です。
行列の積を求める条件は?

行列の積を求める条件は行列の次元が適合していることである。つまり、行列 (A) が (m times n) 行列であり、行列 (B) が (n times p) 行列であるとき、両者の積 (AB) は定義され、結果の行列は (m times p) 行列となる。ここで、行列 (A) の列数は行列 (B) の行数と一致している必要がある。
行列の積の定義と計算
行列の積は、各成分が対応する列と行の内積によって計算される。具体的には、行列 (A = (a_{ij})) と行列 (B = (b_{ij})) の積 (C = AB) の各成分 (c_{ij}) は次のように計算される:
- 行列 (A) の 第 (i) 行の成分をそれぞれ (a_{i1}, a_{i2}, ldots, a_{in}) とする。
- 行列 (B) の 第 (j) 列の成分をそれぞれ (b_{1j}, b_{2j}, ldots, b_{nj}) とする。
- これらの成分の内積を計算する: (c_{ij} = a_{i1}b_{1j} + a_{i2}b_{2j} + cdots + a_{in}b_{nj})。
行列の積の性質
行列の積には特定の性質が存在する。これらの性質は行列の操作において重要である:
- 結合律: (A(BC) = (AB)C) である。
- 分配律: (A(B + C) = AB + AC) および ((A + B)C = AC + BC) である。
- 単位行列との積:任意の行列 (A) に対して、単位行列 (I) に対して (AI = IA = A) である。
行列の積の非可換性
行列の積は一般には 可換でない。つまり、行列 (A) と行列 (B) に対して、一般には (AB neq BA) となる。これは行列の積の計算方法からも明らかである:
- 行列 (A) が (m times n) 行列であり、行列 (B) が (n times m) 行列である場合、積 (AB) は (m times m) 行列となり、積 (BA) は (n times n) 行列となる。
- これらの行列のサイズが異なるため、一般に (AB neq BA) となる。
- ただし、特殊な場合(例えば、両者が正方行列である場合)においても、非可換性が存在する可能性がある。
行列の掛け算ができる条件は?

行列の掛け算ができる条件は、乗算する2つの行列の次元(サイズ)が互いに適切であることである。具体的には、最初の行列の列数が次の行列の行数と一致していなければならない。たとえば、( A )が ( m times n )行列で、( B )が ( n times p )行列であるとき、行列 ( A )と ( B )の積 ( AB )は定義され、結果の行列は ( m times p )行列となる。
行列の次元の整合性
行列の掛け算を行うためには、最初の行列の列数と次の行列の行数が一致しなければならない。この整合性が保たれている場合にのみ、行列の掛け算が定義される。例えば、( A )が ( 2 times 3 )行列で、( B )が ( 3 times 4 )行列であるとき、( A )と ( B )の積 ( AB )は定義され、結果の行列は ( 2 times 4 )行列となる。
- 最初の行列の列数が次の行列の行数と一致する。
- 結果の行列の行数は最初の行列の行数と同じである。
- 結果の行列の列数は次の行列の列数と同じである。
行列の掛け算の計算方法
行列の掛け算は、最初の行列の各行の要素と次の行列の各列の要素との内積を計算することで行われる。具体的には、結果の行列の各要素は、最初の行列の対応する行と次の行列の対応する列の要素の積の和として求められる。たとえば、( A )が ( 2 times 3 )行列で、( B )が ( 3 times 4 )行列であるとき、結果の行列 ( C = AB )の各要素 ( c_{ij} )は次のように計算される。
- 最初の行列の行と次の行列の列の要素の積を計算する。
- 各積の和を求め、結果の行列の各要素に代入する。
- すべての行と列の組み合わせについて上記の計算を繰り返す。
行列の掛け算の適用例
行列の掛け算は、多くの分野で応用されている。例えば、線形代数では、行列の掛け算を使って線形変換を表現する。また、計画法や最適化問題では、行列の掛け算を通じてシステムの状態や制約をモデル化する。さらに、データ分析や機械学習においても、行列の掛け算は特徴量の変換や重みの更新などに利用される。
- 線形変換の表現に用いられる。
- システムの状態や制約のモデル化に使用される。
- 特徴量の変換や重みの更新などに利用される。
よくある質問
行列積の計算順序を減らす一般的な方法は何ですか?
行列積の計算順序を減らす一般的な方法は、行列の次元を分析することです。例えば、3つの行列 A、B、C の積を計算する場合、(AB)C よりも A(BC) の方が計算量が少ない可能性があります。これは、行列の次元が大きく異なる場合に特に効果的です。また、行列の積を計算する前に、行列の形状や特性を考慮して最適な計算順序を決定することで、計算効率を大幅に向上させることができます。
行列のパレタイゼーションとは何ですか?
行列のパレタイゼーションは、行列をより小さなブロックに分割し、それらのブロックを独立して計算する方法です。これにより、並列処理やメモリ効率を改善することができます。例えば、大きな行列を複数の小さな行列に分割し、それぞれを並列に計算することで、全体の計算時間を大幅に短縮することができます。また、メモリ制約のある環境では、小さなブロックを順次処理することで、大規模な行列積の計算を可能にします。
行列積の遅延評価とはどのような方法ですか?
行列積の遅延評価とは、行列の積を実際に計算する代わりに、必要な部分だけを計算する方法です。これは、全ての要素を計算する必要がない場合や、一部の要素のみが必要な場合に特に有用です。遅延評価により、計算リソースを節約し、必要な部分だけを効率的に計算することができます。この方法は、大きな行列の一部のみを頻繁にアクセスするような応用プログラムでよく使用されます。
行列積の最適化に使用される具体的なアルゴリズムは何ですか?
行列積の最適化に使用される具体的なアルゴリズムには、ストラッセンのアルゴリズムや winogradの変形などが挙げられます。ストラッセンのアルゴリズムは、通常の行列乗算よりも少ない乗算回数で行列の積を計算できる方法で、2×2 の行列の積を7回の乗算で計算します。一方、winogradの変形は、乗算の回数を減らす代わりに加算の回数を増やして高速化を図る方法です。これらのアルゴリズムは、特定のサイズや形状の行列に対して特に効果的であり、計算時間を大幅に削減することができます。