等比数列の和の公式をテストする方法!数学証明
等比数列の和の公式は、数学における重要な概念の一つです。この公式を理解し、正しく適用できるようになることは、数学的な問題解決能力を向上させるだけでなく、多くの実際的な状況でも役立ちます。本記事では、等比数列の和の公式をテストする具体的な方法を紹介します。これらの中には、基本的な計算から複雑な証明まで、様々なレベルの問題が含まれています。等比数列の和の公式を深く理解し、その有効性を確認するために、これらを実践的に活用してみてください。

等比数列の和の公式をテストする方法!数学証明
等比数列の和の公式をテストする方法は、数学の基礎的な理解を深め、さまざまな応用に活用できる重要なスキルです。ここでは、等比数列の和の公式のテスト方法と、その数学的な証明について詳しく説明します。
等比数列の定義と基本的な公式
等比数列は、各項が前の項の一定の比(公比)で増加または減少する数列です。等比数列の第 ( n ) 項を ( a n ) とし、初項を ( a )、公比を ( r ) とするとき、等比数列は以下のように表されます: [ a, ar, ar^2, ar^3, ldots, ar^{n-1} ] 等比数列の和 ( S n ) は、初項から第 ( n ) 項までの和を表します。等比数列の和の公式は以下の通りです: [ S n = a frac{1 – r^n}{1 – r} quad (r neq 1) ]
正規表現で連続空白文字を禁止する方法!フォーム改善等比数列の和の公式の証明
等比数列の和の公式を証明するには、以下の手順を踏みます: 1. 等比数列の和を表す: [ S n = a + ar + ar^2 + ar^3 + ldots + ar^{n-1} ] 2. 公比 ( r ) をかけて式を変形する: [ rS n = ar + ar^2 + ar^3 + ldots + ar^{n-1} + ar^n ] 3. 2つの式を引く: [ S n – rS n = a – ar^n ] 4. 左辺を因数分解する: [ S n (1 – r) = a (1 – r^n) ] 5. 両辺を ( 1 – r ) で割る: [ S n = a frac{1 – r^n}{1 – r} quad (r neq 1) ] これで、等比数列の和の公式が証明されました。
等比数列の和の公式をテストする具体例
等比数列の和の公式をテストする具体例をいくつか挙げてみましょう。 例1: 公比が2の等比数列 – 初項 ( a = 1 ) – 公比 ( r = 2 ) – 項数 ( n = 5 ) 公式を適用すると: [ S 5 = 1 frac{1 – 2^5}{1 – 2} = 1 frac{1 – 32}{-1} = 1 times 31 = 31 ] 例2: 公比が0.5の等比数列 – 初項 ( a = 8 ) – 公比 ( r = 0.5 ) – 項数 ( n = 4 ) 公式を適用すると: [ S 4 = 8 frac{1 – (0.5)^4}{1 – 0.5} = 8 frac{1 – 0.0625}{0.5} = 8 frac{0.9375}{0.5} = 8 times 1.875 = 15 ] 例3: 公比が-2の等比数列 – 初項 ( a = 1 ) – 公比 ( r = -2 ) – 項数 ( n = 4 ) 公式を適用すると: [ S 4 = 1 frac{1 – (-2)^4}{1 – (-2)} = 1 frac{1 – 16}{1 + 2} = 1 frac{-15}{3} = 1 times -5 = -5 ] 例4: 公比が1の等比数列 – 初項 ( a = 3 ) – 公比 ( r = 1 ) – 項数 ( n = 6 ) 公式を適用すると: [ S 6 = 3 frac{1 – 1^6}{1 – 1} ] この場合、分母が0になるため、公式は適用できません。ただし、等比数列の和は常に ( 3n ) になります: [ S 6 = 3 times 6 = 18 ] 例5: 公比が-1の等比数列 – 初項 ( a = 2 ) – 公比 ( r = -1 ) – 項数 ( n = 5 ) 公式を適用すると: [ S 5 = 2 frac{1 – (-1)^5}{1 – (-1)} = 2 frac{1 + 1}{1 + 1} = 2 frac{2}{2} = 2 times 1 = 2 ]
等比数列の和の公式の特徴と応用
等比数列の和の公式には、いくつかの特徴があります: 1. 初項と公比が決まれば、和が簡単に計算できる: 公式を用いることで、等比数列の和を直接計算できます。 2. 公比が1の場合は公式が適用できない: 公比が1の等比数列では、公式が適用できません。その場合、和は直接計算されます。 3. 無限等比数列の和の公式: 公比の絶対値が1未満の等比数列の場合は、無限等比数列の和が存在し、その公式は: [ S = frac{a}{1 – r} quad (|r| < 1) ] 4. 数学的な証明: 等比数列の和の公式は、代数学的な手順で証明できます。 5. 応用: 等比数列の和の公式は、金利計算、幾何学的な問題、物理学の問題など、さまざまな分野で応用されます。
等比数列の和の公式の検証方法
等比数列の和の公式の検証方法は以下の通りです: 1. 具体例を用いて検証する: 具体的な数値を代入して、公式が正しく計算されるか確認します。 2. 異なる公比を使用する: 正の公比、負の公比、0.5未満の公比など、さまざまな公比を使用して検証します。 3. 無限等比数列の和の公式を検証する: 公比の絶対値が1未満の場合は、無限等比数列の和の公式を適用し、その結果が正しいか確認します。 4. 代数学的な検証: 代数学的な手順で公式を証明し、その論理的整合性を確認します。 5. 数値的な検証: コンピューターを用いて、大量の数値を計算し、公式が常に正しく適用されるか確認します。
機械学習用トレーニング画像データを自分で収集する方法| 公比 ( r ) | 初項 ( a ) | 項数 ( n ) | 和 ( S n ) |
|---|---|---|---|
| 2 | 1 | 5 | 31 |
| 0.5 | 8 | 4 | 15 |
| -2 | 1 | 4 | -5 |
| 1 | 3 | 6 | 18 |
| -1 | 2 | 5 | 2 |
1 2 4 8 16という数列は?
1 2 4 8 16という数列は等比数列(とうひすうれつ)と呼ばれています。この数列は各項が前の項の2倍になっているものを指します。例えば、1の次が2(1×2)、2の次が4(2×2)、4の次が8(4×2)、8の次が16(8×2)という具合です。この数列は初項と公比(きょうひ)が与えられていれば、任意の項を簡単に計算することができます。
等比数列の定義
等比数列(とうひすうれつ)は、各項が一定の比(公比)を持ち、前の項を一定の数で乗じることで次の項が求まる数列です。この数列の一般項は以下の式で表されます。
- 一般項の式: ( a_n = a_1 times r^{(n-1)} ) ここで、( a_n ) は第 ( n ) 項、( a_1 ) は初項、( r ) は公比です。
- 初項と公比: 1 2 4 8 16の数列では、初項 ( a_1 = 1 ) 、公比 ( r = 2 ) となります。
- 任意の項の計算: 例えば、第5項は ( a_5 = 1 times 2^{(5-1)} = 1 times 2^4 = 16 ) となります。
等比数列の性質
等比数列にはいくつかの重要な性質があります。これらの性質を利用することで、数列の特徴や計算をより理解することができます。
Galaxyで削除された写真を復元する方法!データ復旧- 項の増加: 公比が1より大きい場合、数列は無限に増加します。1 2 4 8 16の数列では、公比が2であるため、項は急速に増加します。
- 項の減少: 公比が1より小さい正值の場合、数列は無限に減少します。例えば、初項が1で公比が0.5の数列は、1 0.5 0.25 0.125 0.0625……という具合に減少します。
- 項の符号: 公比が負の場合、数列の項の符号が交互に変わります。例えば、初項が1で公比が-2の数列は、1 -2 4 -8 16……という具合になります。
等比数列の応用
等比数列は数学や科学の様々な分野で応用されています。以下にいくつかの具体的な例を挙げます。
- 複利計算: 金融における複利計算では、元本が一定の利率で増加する様子を等比数列で表現できます。例えば、1000円を年利率2%で複利で預ける場合、1年後は1000×1.02、2年後は1000×1.022、3年後は1000×1.023 という具合に増加します。
- 生物学での細胞分裂: 細胞分裂の過程では、細胞が一定の周期で2つに分裂します。この過程を等比数列で表現することができます。例えば、1つの細胞が2つに分裂し、それぞれが再び2つに分裂するという過程は、1 2 4 8 16……という数列で表されます。
- コンピュータ科学でのアルゴリズム: コンピュータ科学では、二分探索や再帰的なアルゴリズムなどが等比数列の原理を利用しています。例えば、二分探索では、検索範囲が毎回半分に狭まるため、この過程は等比数列の減少を模倣しています。
1 3 5 7 9の一般項は?
1 3 5 7 9の一般項は2n – 1です。この数列は奇数の列を表していて、各項は1から始めて2ずつ増えていきます。つまり、この数列のn番目の項は2n – 1で表されます。
奇数列の性質
奇数列は、1から始めて2ずつ増える数の列を指します。この列は、任意の自然数nについて2n – 1という一般項で表される特性を持っています。
行列積の計算順序を減らす方法!高速化テクニック- この列は常に奇数を生成します。
- 各項は2ずつ増えていきます。
- この数列は無限に続くことができます。
一般項の導出方法
一般項2n – 1は、数列1 3 5 7 9の特性を数学的に表したものです。この一般項を導出するためには、以下のような手順を踏みます。
- 第1項は1です。
- 第2項から第1項との差は2です。
- したがって、n番目の項は1 + 2(n-1)と表すことができます。
- 簡略化すると2n – 1となります。
具体例と応用
1 3 5 7 9の一般項2n – 1は、さまざまな場面で応用することができます。例えば、以下のような具体例があります。
- 第5項を求める:2(5) – 1 = 9
- 第10項を求める:2(10) – 1 = 19
- 第50項を求める:2(50) – 1 = 99
等比数列の公比の求め方は?

等比数列の公比(比例定数)を求めたい場合、次に示す方法を使用します。
等比数列は、各項が前の項と一定の比率で増加または減少する数列です。公比を ( r ) とすると、等比数列の第1項を ( a ) とし、第2項を ( ar )、第3項を ( ar^2 ) と表すことができます。
公比 ( r ) を求めるには、以下の手順を踏みます:
1. 等比数列の 2つ の 連続する項 を選びます。例えば、第2項と第3項を選びます。
2. その2つの項の 比 を計算します。具体的には、第3項を第2項で割ります。つまり、 ( r = frac{ar^2}{ar} = frac{a_3}{a_2} ) です。
3. この比が公比 ( r ) となります。
等比数列の公比の定義
等比数列の公比とは、各項が前の項と一定の比率で増加または減少する 比率 のことです。等比数列の第1項を ( a )、公比を ( r ) とすると、第2項は ( ar )、第3項は ( ar^2 ) となります。この比率 ( r ) が等比数列の公比であり、各項間の関係を決定します。
公比の計算例
等比数列の例として、数列 2, 6, 18, 54, … を考えます。
1. 第2項は 6、第3項は 18 です。
2. 公比 ( r ) を計算します: ( r = frac{18}{6} = 3 )。
3. この数列の公比は 3 であることがわかります。
公比の応用:逆数の性質
等比数列の公比 ( r ) は、数列の各項間の比率を示しますが、公比の逆数も重要な概念です。例えば、公比が 3 の等比数列の場合、公比の逆数は ( frac{1}{3} ) です。逆数を使うことで、数列の逆順の公比を求めることができます。例えば、数列 54, 18, 6, 2 の公比は ( frac{1}{3} ) になります。
1. 第2項は 18、第1項は 54 です。
2. 公比の逆数 ( r ) を計算します: ( r = frac{18}{54} = frac{1}{3} )。
3. この数列の公比の逆数は ( frac{1}{3} ) であることがわかります。
等差数列の和はどうやって求める?
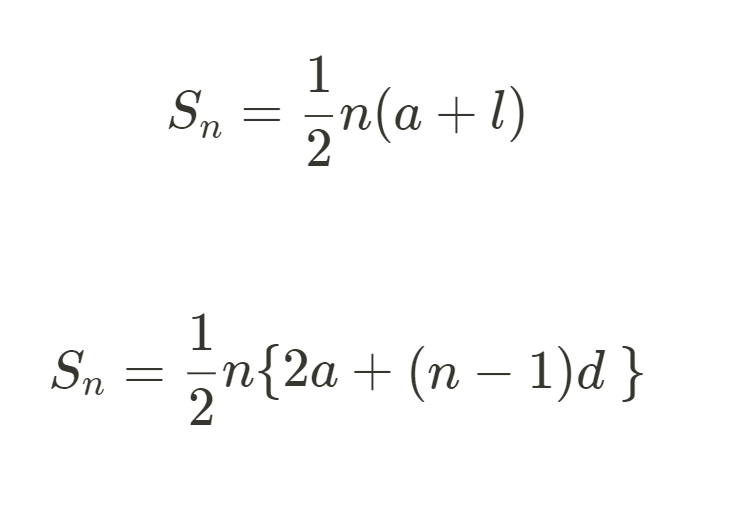
等差数列の和は次のように求める:
等差数列の和 ( S_n ) は、初項 ( a )、公差 ( d )、項数 ( n ) が与えられたとき、以下の公式で求められます。
[ S_n = frac{n}{2} left( 2a + (n-1)d right) ]
また、等差数列の和は、初項と最終項 ( l ) を用いて次のようにも表現できます。
[ S_n = frac{n}{2} (a + l) ]
ここで、最終項 ( l ) は ( a + (n-1)d ) で求められます。
等差数列の和の求め方: 初歩的な説明
等差数列の和を求める基本的な手順は以下の通りです。
- まず、等差数列の初項 ( a )、公差 ( d )、項数 ( n ) を確認します。
- 次に、公式 ( S_n = frac{n}{2} left( 2a + (n-1)d right) ) を使用して、和 ( S_n ) を計算します。
- または、最終項 ( l ) を ( a + (n-1)d ) で計算し、公式 ( S_n = frac{n}{2} (a + l) ) を使用します。
等差数列の和の公式の導出方法
等差数列の和の公式の導出方法は以下の通りです。
- 等差数列の各項を ( a, a+d, a+2d, ldots, a+(n-1)d ) と表します。
- これらの項を順番に並べた数列と逆順に並べた数列を足し合わせると、全ての項が ( a + l ) になります。
- したがって、数列全体の和は ( n ) 個の ( a + l ) の半分に等しくなり、これを式で表すと ( S_n = frac{n}{2} (a + l) ) となります。
等差数列の和の応用例
等差数列の和の公式は、実際の問題解決に広く応用できます。
- 例えば、最初の100個の自然数の和を求めたい場合、初項 ( a = 1 )、公差 ( d = 1 )、項数 ( n = 100 ) を使用し、公式 ( S_n = frac{100}{2} (1 + 100) = 5050 ) で求めます。
- また、ある月の日数が31日の場合、1日目から31日目の日にちの和も等差数列の和として計算できます。
- さらに、等差数列の和の公式は、財務管理やプロジェクト計画における累積値の計算に利用されます。
よくある質問
等比数列の和の公式をテストする利点は何ですか?
利点として、等比数列の和の公式をテストすることで、計算の正確性を確認できます。また、このプロセスは、数列の性質を深く理解する教育的な役割も果たします。テストを通じて、学生は公式の適用方法を学び、複雑な数学的問題を解決するスキルを磨くことができます。
等比数列の和の公式をテストする具体的な方法は?
具体的な方法としては、まず、異なる比(公比)と項数を持つ等比数列をいくつか準備します。次に、公式を用いて和を計算し、その結果を手動計算や他の方法で得た結果と比較します。一致すれば、公式が正しく適用できていることを確認できます。また、エクセルやプログラミング言語を使用することで、より効率的にテストを行うことも可能です。
等比数列の和の公式をテストする際の一般的な誤解は?
一般的な誤解としては、公式の適用範囲が制限されていることを認識していないことがあります。例えば、公比が1の場合や、無限等比数列の和を求める際には、特別な注意が必要です。また、公式を機械的に適用するのではなく、数列の性質を理解することが重要です。これによって、誤った結果を避けることができます。
等比数列の和の公式のテスト結果が予想と異なる場合、どのように対処すべきか?
テスト結果が予想と異なる場合、まず計算プロセスを再検討し、誤ったステップがないか確認します。公式の適用に問題がない場合でも、数列の定義や条件に誤りがないか確認することが重要です。必要に応じて、他の方法で再計算を行い、結果の一致を確認することも有効です。それでも解決しない場合は、専門家に相談することを検討しましょう。