欠落桁、丸め誤差…計算精度向上のテクニックを解説
計算の精度を向上させるテクニックは、特に大規模なデータ処理や科学技術計算において重要です。欠落桁や丸め誤差は、計算結果の信頼性を大きく損なう要因となります。本記事では、これらの問題を効果的に解決する方法を解説します。具体的には、高精度な数値計算ライブラリの利用、アルゴリズムの最適化、そして誤差伝播の抑制方法について詳しく説明します。これにより、より正確で信頼性の高い計算結果を得られるようになるでしょう。

計算精度向上のための基本テクニック
計算精度を向上させるためには、欠落桁や丸め誤差などの問題を理解し、適切な対策を講じることが必要です。これらの問題は、特に浮動小数点演算や大規模なデータ処理において顕著に現れます。以下のセクションでは、具体的なテクニックとその適用方法について詳しく解説します。
欠落桁の理解と対策
欠落桁は、数値が持つ有効桁数が不足した状態を指します。例えば、10進数の0.1は2進数では無限小数になるため、浮動小数点数として表現すると精度が低下します。欠落桁を防ぐためのテクニックには以下のようなものがあります:
阪神バスの運行状況をリアルタイムで確認する方法- 精度の高いデータ型の使用:double型やlong double型を使用することで、より多くの有効桁数を保持できます。
- 任意精度演算ライブラリの利用:GMPやMPFRのような任意精度演算ライブラリを使用することで、任意の桁数での計算が可能になります。
- 数値の再スケーリング:計算前に数値を大きくしたり小さくしたりする再スケーリングを行うことで、有効桁数を確保できます。
| テクニック | 説明 |
|---|---|
| 精度の高いデータ型の使用 | double型やlong double型を使用することで、より多くの有効桁数を保持できます。 |
| 任意精度演算ライブラリの利用 | GMPやMPFRのような任意精度演算ライブラリを使用することで、任意の桁数での計算が可能になります。 |
| 数値の再スケーリング | 計算前に数値を大きくしたり小さくしたりする再スケーリングを行うことで、有効桁数を確保できます。 |
丸め誤差の理解と対策
丸め誤差は、数値を有限の桁数に丸めたときに発生する誤差を指します。例えば、0.1 + 0.2の結果が0.3にならないことはよく知られています。丸め誤差を最小限に抑えるためのテクニックには以下のようなものがあります:
- 丸めモードの設定:CPUや言語の設定で、丸めモードを指定することで、丸め誤差の影響をコントロールできます。
- 途中結果の保持:中間結果を高い精度で保持し、最終的に結果を丸める方法があります。
- 累积演算の順序変更:加算や乗算の順序を変えることで、丸め誤差が累積するのを防ぐことができます。
| テクニック | 説明 |
|---|---|
| 丸めモードの設定 | CPUや言語の設定で、丸めモードを指定することで、丸め誤差の影響をコントロールできます。 |
| 途中結果の保持 | 中間結果を高い精度で保持し、最終的に結果を丸める方法があります。 |
| 累积演算の順序変更 | 加算や乗算の順序を変えることで、丸め誤差が累積するのを防ぐことができます。 |
数値安定性の向上
数値安定性は、計算が小さな入力の変動に対しても大きく変化しないことを指します。数値安定性を向上させるためのテクニックには以下のようなものがあります:
- 条件数の評価:条件数を評価することで、問題の数値的安定性を確認できます。
- 反復改善:反復的な計算を行い、結果を徐々に改善していく方法があります。
- アルゴリズムの選択:数値的に安定したアルゴリズムを選択することで、計算精度を向上させることができます。
| テクニック | 説明 |
|---|---|
| 条件数の評価 | 条件数を評価することで、問題の数値的安定性を確認できます。 |
| 反復改善 | 反復的な計算を行い、結果を徐々に改善していく方法があります。 |
| アルゴリズムの選択 | 数値的に安定したアルゴリズムを選択することで、計算精度を向上させることができます。 |
並列計算における精度向上
並列計算では、複数のプロセッサやコアが同時に計算を実行します。並列計算における精度向上には以下のようなテクニックが有効です:
- 同期の制御:各プロセッサ間の同期を適切に制御することで、精度低下を防ぎます。
- データの分散:データを適切に分散させ、各プロセッサが負担均等に計算を行えるようにします。
- 結果の集約:計算結果を効率的に集約することで、最終的な精度を向上させます。
| テクニック | 説明 |
|---|---|
| 同期の制御 | 各プロセッサ間の同期を適切に制御することで、精度低下を防ぎます。 |
| データの分散 | データを適切に分散させ、各プロセッサが負担均等に計算を行えるようにします。 |
| 結果の集約 | 計算結果を効率的に集約することで、最終的な精度を向上させます。 |
ソフトウェアとハードウェアの選択
計算精度を向上させるためには、ソフトウェアとハードウェアの適切な選択も重要です。以下のポイントに注意することが推奨されます:
変数代入の基礎[初心者向け解説]プログラミング入門- プログラミング言語の選択:精度に優れたライブラリや機能を備えたプログラミング言語を選択します。
- ハードウェアの選択:精度に優れたCPUやFPGAなどのハードウェアを選択します。
- 並列計算向けのハードウェア:GPUやTPUなどの並列計算向けハードウェアを活用します。
| テクニック | 説明 |
|---|---|
| プログラミング言語の選択 | 精度に優れたライブラリや機能を備えたプログラミング言語を選択します。 |
| ハードウェアの選択 | 精度に優れたCPUやFPGAなどのハードウェアを選択します。 |
| 並列計算向けのハードウェア | GPUやTPUなどの並列計算向けハードウェアを活用します。 |
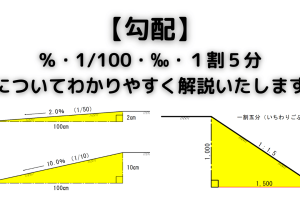
桁落ちはなぜダメなのでしょうか?
![]()
桁落ちは、数値やデータの精度を大幅に低下させるため、多くの分野で問題とされています。特に、科学、工学、金融などの精密な計算を必要とする分野では、桁落ちが発生すると重大なエラーや誤差が生じる可能性があります。例えば、金融取引では、小さな誤差が大きな損失につながる可能性があり、科学的実験では、結果の信頼性が著しく低下します。このため、桁落ちを避けるための様々な手法が開発されています。
桁落ちの原因とメカニズム
桁落ちの主な原因は、数値の有限な表現と演算の制限にあります。計算機は数値を有限の桁数で表現するため、非常に大きな数や非常に小さな数を扱う際に、情報が失われる可能性があります。例えば、2つの非常に異なる大きさの数値を足し算或いは引算すると、小さな数が丸め誤差によって消失することがあります。この現象は、浮動小数点数の有限な桁数が原因で発生します。
- 数値の有限な表現: 計算機は数値を有限の桁数で表現するため、情報が失われる。
- 演算の制限: 大きな数と小さな数の演算では、小さな数が丸め誤差によって消失。
- 浮動小数点数の制限: 浮動小数点数の有限な桁数が桁落ちを引き起こす。
桁落ちの影響
桁落ちが発生すると、さまざまな影響が生じます。まず、結果の精度が大幅に低下し、予期せぬ誤差が生じることがあります。これは、特に繰り返し計算や長時間のシミュレーションを行う場合に顕著です。また、桁落ちはアルゴリズムの安定性を損なう可能性があり、計算結果が不安定になったり、収束しなくなることがあります。さらに、桁落ちは信頼性を低下させ、計算結果の信頼性が保て是韩国人なくなります。
勾配の基本と計算ツール!建築設計に役立つ- 結果の精度の低下: 桁落ちにより、予期せぬ誤差が生じ、結果の精度が大幅に低下。
- アルゴリズムの安定性の損なわれ: 桁落ちは計算結果の不安定性や収束の失敗を引き起こす。
- 信頼性の低下: 桁落ちにより、計算結果の信頼性が保てなくなり、信頼性が低下。
桁落ちを避ける方法
桁落ちを避けるためには、几种類の手法が用いられます。まず、数値のスケーリングを行うことで、大きな数と小さな数の差を小さくすることができます。また、高精度なデータ型を使用することで、数値の表現範囲を広げ、桁落ちを抑制できます。さらに、演算順序の最適化も有効で、計算の順序を工夫することで、桁落ちのリスクを低減することができます。
- 数値のスケーリング: 大きな数と小さな数の差を小さくすることで、桁落ちを抑制。
- 高精度なデータ型の使用: 渡営浮動小数点数や任意精度算術を使用することで、数値の表現範囲を広げる。
- 演算順序の最適化: 計算の順序を工夫することで、桁落ちのリスクを低減。
有限桁に入りきらない部分の数値に対して四捨五入、切り上げ、切り捨てのいずれかを行う事で生じる誤差を何というか答えなさい。?
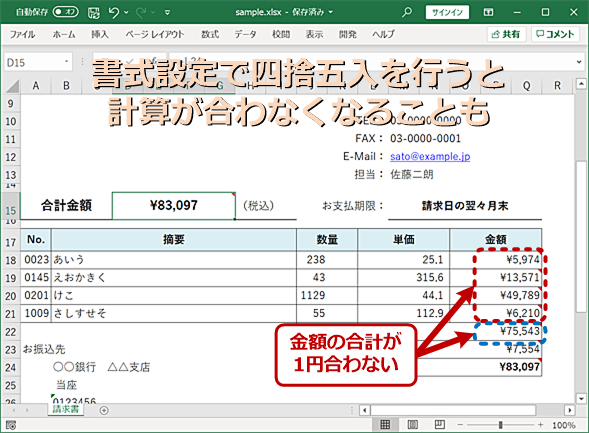
有限桁に入りきらない部分の数値に対して四捨五入、切り上げ、切り捨てのいずれかを行うことで生じる誤差を丸め誤差または丸め誤差(ラウンドオフ誤差)と呼びます。
丸め誤差の定義
丸め誤差とは、有限桁数の制限により数値を四捨五入、切り上げ、または切り捨てることで生じる誤差のことを指します。具体的には、浮動小数点数の計算や有理数の近似などで頻繁に見られます。この誤差は、数値の有効桁数が限られているため、理論的に正確な値と実際の計算結果が異なることを示します。
Androidで許可なくアプリをインストールさせない設定- 浮動小数点数の計算では、有限の桁数で表現できない数値が存在します。
- 有理数の近似では、分数を小数に変換した際に無限に続く数値が発生することがあります。
- 計算機では、有限のメモリと処理能力の制限により、丸めが必要となる場合があります。
丸め誤差の影響
丸め誤差が生じることで、計算結果の精度が低下し、予期せぬ結果を招くことがあります。特に、反復計算や累積誤差が発生する場合は、誤差が蓄積され、最終的な結果に大きな影響を与える可能性があります。
- 反復計算では、小さな丸め誤差が積み重なり、大きな誤差につながることがあります。
- 累積誤差は、多次元の計算や複雑なアルゴリズムで特に問題となります。
- 科学計算や金融計算などの精密な分野では、丸め誤差の影響を最小限に抑えることが重要です。
丸め誤差の対策
丸め誤差の影響を最小限に抑えるためには、いくつかの対策が考えられます。例えば、高精度な数値型を使用したり、アルゴリズムの改善や誤差補正などの手法が有効です。
- 高精度な数値型を使用することで、より多くの桁数を扱うことができます。
- アルゴリズムの改善では、計算手順を見直し、丸め誤差が蓄積しにくい方法を採用します。
- 誤差補正では、計算結果を補正するための補正項を導入します。
打ち切り誤差の対策は?

打ち切り誤差は、数値計算において値を丸めるときに発生する誤差です。これを最小限に抑えるためには、いくつかの対策が考えられます。まず、計算の精度を向上させることが重要です。計算に使用するデータの桁数を増やす、または高精度のアルゴリズムを利用するなど、計算の途中で発生する誤差を小さくすることができます。次に、丸め方を適切に選択することも効果的です。例えば、四捨五入や切り捨て、切り上げなどの異なる丸め方を用いることで、全体の誤差を調整することが可能です。さらに、誤差の伝播を抑制する方法も考慮すべきです。計算の順序や方法を工夫することで、誤差が最終結果に大きく影響することを防ぐことができます。
精度向上の方法
高精度の計算を行うためには、以下の方法が有効です:
- 倍精度浮動小数点数を使用する:倍精度浮動小数点数は、通常の浮動小数点数よりも桁数が多いため、より精度の高い計算ができます。
- 多倍長精度計算ライブラリを利用する:多倍長精度計算ライブラリ(例:GNU MPFR)は、任意の桁数で計算を行うことができ、非常に高い精度を実現します。
- 誤差補正技術を適用する:数値解析における誤差補正技術(例:Kahan summation algorithm)を使用することで、計算過程での誤差を補正することができます。
丸め方の選択
丸め方によって最終的な結果の誤差が大幅に変わるため、適切な丸め方を選ぶことが重要です:
- 四捨五入:最も一般的な丸め方で、0.5以上は切り上げ、0.5未満は切り捨てます。一貫性があり、誤差のバランスが取れます。
- 銀行家四捨五入:0.5の場合、偶数の桁に丸める方法です。これにより、丸めのバイアスが減少します。
- 切り上げ/切り捨て:特定の状況や目的に応じて、常に切り上げまたは切り捨てを行う場合があります。
誤差伝播の抑制
誤差が計算過程で伝播するのを防ぐための方法を紹介します:
- 計算順序の最適化:計算の順序を変更することで、誤差が累積しにくい順序で計算を行うことができます。
- 途中経過の保存と再使用:途中の計算結果を高い精度で保存し、後で再使用することで、再計算時の誤差を減らすことができます。
- 迭代法の利用:誤差の緩和や制御に効果的な迭代法(例:Newton-Raphson法)を使用することで、最終結果の精度を向上させることができます。
丸め誤差をなくす方法は?

丸め誤差をなくす方法は、数値をより正確に扱うための様々なテクニックを使用することです。例えば、浮動小数点数ではなく固定小数点数を使用することで、丸め誤差を大幅に軽減できます。また、数値演算ライブラリを使用することで、内部で高精度の演算が行われ、結果の精度が向上します。さらに、数値の表現方法を変更することも有効です。例えば、分数や対数を使用することで、特定の問題において丸め誤差を抑えられる場合があります。以下のセクションでは、具体的な方法について詳しく説明します。
1. 固定小数点数の使用
固定小数点数を使用することで、丸め誤差を避けることができます。固定小数点数とは、小数点の位置が常に固定されている数値表現形式です。これにより、浮動小数点数のような動的な小数点位置による丸め誤差が発生しません。固定小数点数は、特に金銭計算や他の精度が必要な分野で広く使用されています。以下に、固定小数点数を使用する利点をまとめます:
- 高精度:固定小数点数は、特定の範囲内での数値を正確に表現できます。
- 一貫性:小数点位置が固定されているため、計算結果の一貫性が保てます。
- 高速性:ハードウェアレベルでの演算が効率的に行えるため、パフォーマンスが向上します。
2. 高精度数値演算ライブラリの利用
数値演算ライブラリを使用することで、内部的に高精度の計算が行われ、丸め誤差を軽減します。これらのライブラリは、多倍長精度の数値を扱うことができ、従来の浮動小数点数では難しいような高精度の計算を可能にします。代表的な高精度数値演算ライブラリには、Pythonの`decimal`モジュールや、C++の`GMP`ライブラリなどがあります。以下に、高精度数値演算ライブラリの利点をまとめます:
- 高精度:多倍長精度の数値を扱うことで、丸め誤差を大幅に削減できます。
- 柔軟性:様々な数値表現形式をサポートしており、用途に応じて選択できます。
- 信頼性:広く使用されており、信頼性が高く、テストが十分に行われています。
3. 数値表現の変更
数値の表現方法を変更することも、丸め誤差を抑える有効な手段の一つです。例えば、分数や対数を使用することで、特定の問題において精度を向上させることができます。分数は、有理数を正確に表現でき、対数は、計算の範囲を制限することで誤差を減らすことができます。以下に、数値表現の変更による利点をまとめます:
- 正確性:分数は有理数を正確に表現でき、対数は計算の範囲を制限します。
- 効率性:特定の問題では、分数や対数を使用することで計算の効率が向上します。
- 特定用途への適応:分数や対数は、特定の分野(例:音楽の周波数計算)で特に有用です。
よくある質問
なぜ欠落桁や丸め誤差が発生するのか?
欠落桁や丸め誤差が発生する理由は、数値がコンピュータで表現できる限られた範囲と精度を超える場合があります。たとえば、浮動小数点数は固定されたビット数で表現されるため、非常に大きな数や非常に小さな数を正確に表現することができません。また、某些数(例:1/3)は10進数では有限の桁数で表現できますが、2進数では無限に続く数となり、そのため丸めが行われ、誤差が生じます。
欠落桁や丸め誤差を避ける方法は何か?
欠落桁や丸め誤差を完全に避けるのは難しいですが、いくつかのテクニックを使用することで誤差を最小限</strongに抑えることができます。例えば、数値のスケーリングを行うと、非常に大きな数や小さな数を扱う際に精度を保つことができます。また、浮動小数点数の代わりに固定小数点数や任意精度算術を使用することで、より正確な計算が可能になります。また、数学的な解析によって誤差の範囲を事前に把握し、それに基づいてアルゴリズムを最適化</strongすることも重要です。
どのようなテクニックが計算精度の向上に有効か?
計算精度を向上させるためのテクニックには、高精度なデータ型の使用、アルゴ lithmicの選択と最適化、数値安定性の確保などが挙げられます。高精度なデータ型としては、任意精度算術ライブラリを使用した多倍長精度計算が有効です。アルゴリズムの選択と最適化では、誤差が累積しにくいアルゴリズムを選択したり、計算順序を調整したりすることで精度を向上させることができます。また、数値安定性を確保するためには、条件付き数(条件数)が小さくなるようにパラメータを設定することが重要です。
具体例として、どのようなシナリオでこれらのテクニックが活用されるのか?
これらのテクニックは、特に科学計算や金融計算で重要な役割を果たします。たとえば、気象予報では、大規模な数値シミュレーションが行われ、微小な誤差が結果に大きな影響を及ぼす可能性があるため、高精度な計算が求められます。金融分野では、取引価格やリスク評価などの高精度な計算が必要で、小さな誤差が大きな損失につながる可能性があるため、これらのテクニックを用いて精度を確保しています。また、宇宙科学や量子力学などの先端的な分野でも、これらのテクニックが活用されています。

![変数代入の基礎[初心者向け解説]プログラミング入門 14 変数代入の基礎[初心者向け解説]プログラミング入門](https://mahinamaeda.com/wp-content/uploads/-67d61539f11a3-7872-300x200.jpg)